The introduction of deep convolutional neural networks (CNNs) has dramatically improved image recognition capabilities. Among the seminal architectures, the VGG (Visual Geometry Group) Network, proposed by Karen Simonyan and Andrew Zisserman in 2014, was a breakthrough. It demonstrated the effectiveness of deep, simple, and uniform layer structures in achieving state-of-the-art performance on the ImageNet dataset.
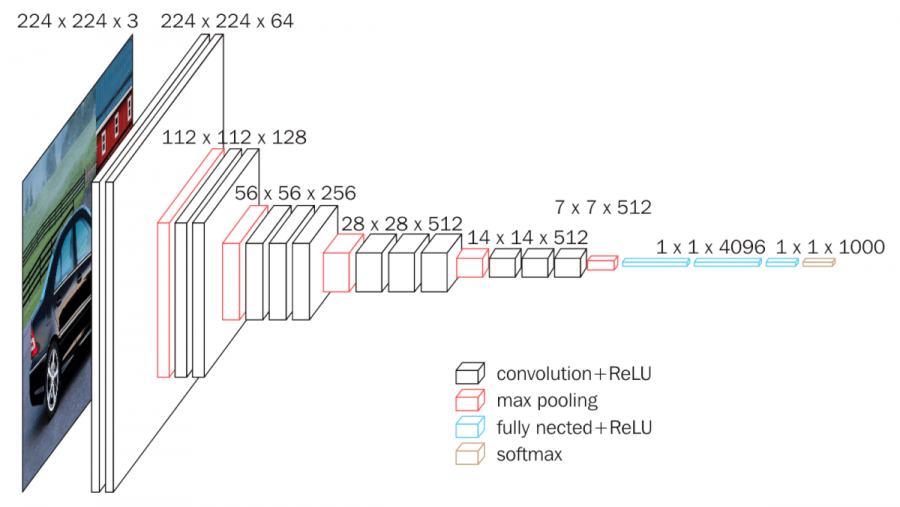
VGG Architecture Overview
The hallmark of VGG lies in its simplicity and depth. The architecture systematically increases the depth of the network by stacking small convolutional filters (3×3 kernels) while maintaining a consistent structure across layers. This design enables the network to learn hierarchical features effectively, from simple edges in shallow layers to complex patterns in deeper ones.
Design Principles
Uniform Convolutional Layers:
- VGG exclusively uses 3×3 filters with a stride of 1 and padding of 1.
- These filters minimize computational complexity while ensuring that each convolutional layer extracts features within a small receptive field.
Max-Pooling for Down-Sampling:
- 2×2 max-pooling layers with a stride of 2 follow blocks of convolutional layers.
- This down-sampling strategy reduces spatial dimensions progressively, allowing the network to focus on high-level features.
Deep Stack of Convolutional Blocks:
- Each convolutional block contains multiple convolutional layers followed by a pooling layer.
- The number of filters in convolutional layers doubles after each pooling operation (e.g., 64, 128, 256, 512).
Fully Connected Layers:
- After convolutional and pooling layers, the spatial features are flattened and passed through three fully connected layers, ending with a softmax layer for classification.
Detailed VGG Variants
VGG-16
VGG-16 is one of the most well-known variants, comprising:
- 13 convolutional layers across 5 blocks.
- 3 fully connected layers.
- 138 million parameters.
Architecture:
| Block | Convolution Layers | Kernel Size | Filters | Output Shape |
|---|---|---|---|---|
| 1 | 2 | 3×3 | 64 | 224×224×64 |
| 2 | 2 | 3×3 | 128 | 112×112×128 |
| 3 | 3 | 3×3 | 256 | 56×56×256 |
| 4 | 3 | 3×3 | 512 | 28×28×512 |
| 5 | 3 | 3×3 | 512 | 14×14×512 |
| FC | Fully Connected | N/A | N/A | 4096, 4096, 1000 |
Training Insights
Weight Initialization:
- VGG networks are trained from scratch with Gaussian initialization for weights and biases set to zero.
- Using Xavier or He initialization can further stabilize the training process.
Activation Functions:
- ReLU (Rectified Linear Unit) is used to introduce non-linearity, accelerating convergence and avoiding vanishing gradient issues.
Batch Normalization:
- Although not part of the original VGG, modern implementations often integrate batch normalization layers to stabilize learning and improve generalization.
Optimization:
- Trained using Stochastic Gradient Descent (SGD) with momentum.
- A learning rate schedule reduces the learning rate after plateaus in validation accuracy.
Loss Function:
- Cross-entropy loss is used to measure the discrepancy between predicted probabilities and ground truth labels.
Why Depth Matters
VGG demonstrated that increasing the network’s depth allows it to learn hierarchical feature representations more effectively.
Feature Hierarchy:
- Early layers capture low-level features like edges and textures.
- Intermediate layers focus on shapes and objects.
- Deep layers identify semantic concepts like faces or animals.
Receptive Field Expansion:
- The depth allows small kernels (3×3) to incrementally expand the receptive field. For example, stacking three 3×3 filters covers the same area as a 7×7 kernel but retains more parameters to model complex patterns.
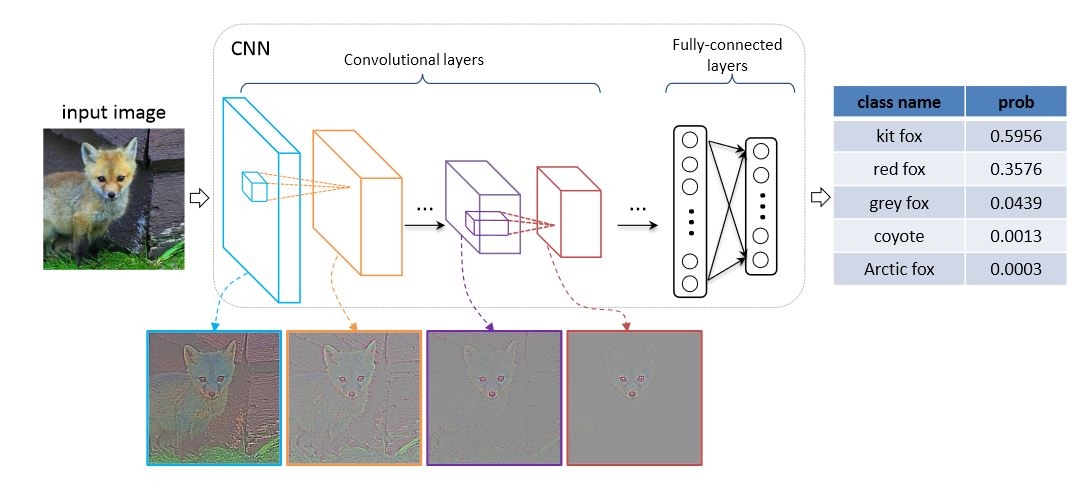
Computational Complexity
The key limitation of VGG lies in its computational demand:
Parameter Count:
- VGG-16 has 138 million parameters, leading to large memory requirements and slow inference on resource-constrained systems.
Redundancy:
- The fully connected layers alone account for a significant portion of parameters, introducing redundancy in feature representation.
Training Time:
- Due to its depth and high parameter count, training requires powerful hardware (e.g., GPUs) and long periods to converge.
Technical Comparisons with Successors
While VGG revolutionized image recognition, its limitations led to the development of more efficient architectures like ResNet, Inception, and EfficientNet:
Residual Connections (ResNet):
- ResNet mitigates the vanishing gradient problem by introducing skip connections, enabling networks to go even deeper.
Multi-Scale Filters (Inception):
- Inception employs filters of varying sizes in parallel to capture features at multiple scales, reducing redundancy.
Compound Scaling (EfficientNet):
- EfficientNet optimizes network width, depth, and resolution using a compound scaling strategy for higher efficiency.
Implementing VGG with Code
Here’s a simple PyTorch implementation of VGG-16:
import torch
import torch.nn as nn
class VGG16(nn.Module):
def __init__(self, num_classes=1000):
super(VGG16, self).__init__()
self.features = nn.Sequential(
# Block 1
nn.Conv2d(3, 64, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.Conv2d(64, 64, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2),
# Block 2
nn.Conv2d(64, 128, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.Conv2d(128, 128, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2),
# Block 3
nn.Conv2d(128, 256, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.Conv2d(256, 256, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.Conv2d(256, 256, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2),
# Block 4
nn.Conv2d(256, 512, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.Conv2d(512, 512, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.Conv2d(512, 512, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2),
# Block 5
nn.Conv2d(512, 512, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.Conv2d(512, 512, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.Conv2d(512, 512, kernel_size=3, padding=1), nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.classifier = nn.Sequential(
nn.Linear(512*7*7, 4096), nn.ReLU(inplace=True), nn.Dropout(),
nn.Linear(4096, 4096), nn.ReLU(inplace=True), nn.Dropout(),
nn.Linear(4096, num_classes)
)
def forward(self, x):
x = self.features(x)
x = torch.flatten(x, 1)
x = self.classifier(x)
return x
# Instantiate model
model = VGG16(num_classes=1000)
print(model)
Advantages of VGG
Depth-Powered Performance: By increasing depth systematically, VGG achieved state-of-the-art performance during its introduction.
Transfer Learning: Due to its general feature extraction capabilities, VGG is widely used as a pre-trained model for various tasks, including object detection and segmentation.
Simplicity and Generalization: VGG’s uniform design makes it adaptable and easy to use, even in customized architectures.
Limitations of VGG
Despite its revolutionary design, VGG has limitations:
Computational Costs: With millions of parameters, VGG requires significant computational resources for training.
Memory Consumption: The high parameter count leads to large model sizes, making VGG unsuitable for edge devices or resource-constrained environments.
Performance Bottlenecks: Newer architectures like ResNet and Inception surpassed VGG by introducing techniques like skip connections and multi-scale feature extraction, which reduce computation while improving accuracy.
VGG’s Legacy in Modern AI
Though newer architectures have outpaced VGG in efficiency and accuracy, its legacy is undeniable. Here’s how VGG continues to impact the field:
Foundation for Transfer Learning: VGG models, pre-trained on ImageNet, are still widely used in various applications. Researchers fine-tune these models to solve domain-specific problems with limited data.
Inspiration for Depth-Oriented Architectures: VGG’s success demonstrated the value of depth in CNNs, inspiring architectures like ResNet, DenseNet, and EfficientNet, which build on its principles.
Use in Feature Extraction: The hierarchical features learned by VGG are leveraged for non-classification tasks like style transfer and image captioning.
Applications of VGG in Real-World Scenarios
Medical Imaging: VGG has been employed to classify X-rays, detect tumors in MRI scans, and identify diseases in histopathology images.
Autonomous Vehicles: VGG-based models contribute to object detection systems in self-driving cars, recognizing pedestrians, vehicles, and traffic signs.
Facial Recognition: VGG’s feature extraction capabilities are utilized in facial recognition systems for security and authentication.
Art and Creativity: VGG underpins applications like neural style transfer, blending the features of an image with artistic styles.
Conclusion
The VGG architecture laid the foundation for deep CNNs by showing that depth, coupled with simplicity, could achieve remarkable results. While its computational demands have been surpassed by modern architectures, VGG’s influence on network design and feature learning remains a cornerstone in computer vision. For practitioners, understanding VGG is essential for mastering the evolution of CNNs and applying deep learning to complex image recognition tasks.
