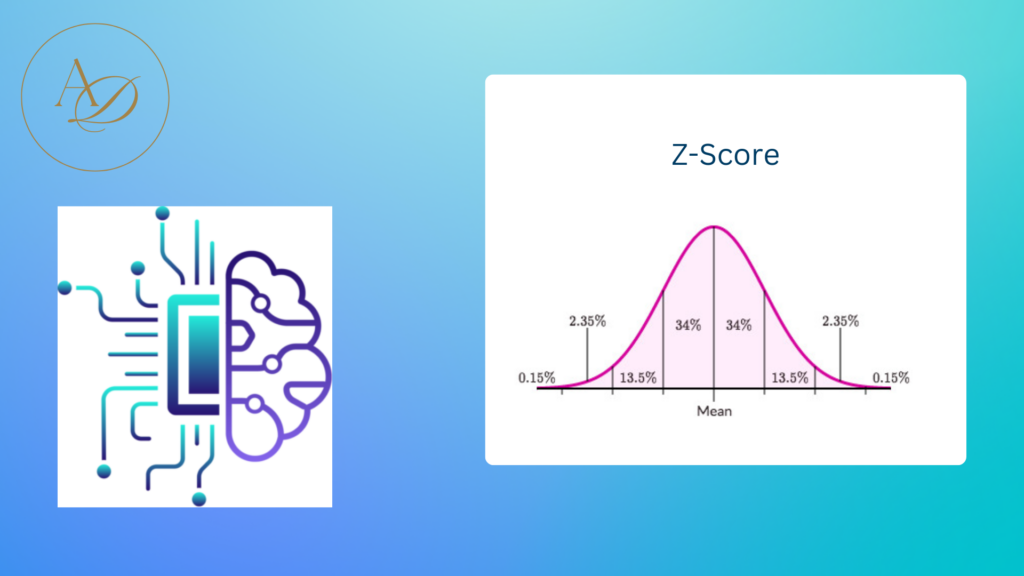
In the vast realm of statistics, there exists a powerful tool known as the Z-score. Whether you’re a seasoned data scientist or just starting to dip your toes into the world of statistics, understanding the Z-score can prove invaluable in various analytical endeavors.
What is a Z-Score?
In simple terms, a Z-score measures the number of standard deviations a data point is from the mean of a dataset. It’s a way to standardize data and determine how far, in standard deviation units, a particular value is from the mean of the dataset. This normalization process enables comparisons across different datasets, regardless of their original units or scales.
Mathematically, the formula for calculating the Z-score of a data point, (), given a dataset with mean, (
), and standard deviation, (
), is:
Here, () represents the Z-score.
Understanding the Significance
Now, you might be wondering, “Why do we need to bother with Z-scores?” Well, Z-scores serve several crucial purposes in statistical analysis:
- Normalization: As mentioned earlier, Z-scores normalize data, making it easier to compare values from different datasets. By standardizing data, analysts can identify outliers, trends, and patterns more effectively.
- Identification of Outliers: Outliers, or data points that deviate significantly from the rest of the dataset, can skew statistical analyses. Z-scores help in identifying these outliers by flagging data points that fall beyond a certain threshold, typically set at (Z =
3) (indicating three standard deviations away from the mean).
- Probability Calculations: Z-scores are closely tied to probabilities in a normal distribution. For instance, given a standard normal distribution (mean = 0, standard deviation = 1), Z-scores can be used to calculate the probability of observing a value below, above, or between certain thresholds.
- Hypothesis Testing: In hypothesis testing, Z-scores play a pivotal role, especially when dealing with large sample sizes. They help in determining whether a sample mean is significantly different from a population mean, thereby aiding in decision-making processes.
For Hypothesis Testing
When conducting hypothesis tests or constructing confidence intervals for the population mean (\(\mu\)) based on a sample mean (\(\bar{x}\)), the Z-score is calculated using the formula:
Here’s what each component represents:
– (): The sample mean.
– (): The population mean (the value being tested or estimated).
– (): The population standard deviation.
– (): The sample size.
The expression calculates the standard error of the mean. It indicates the average amount by which the sample mean is likely to deviate from the population mean due to random sampling variability.
The Z-score tells us how many standard deviations the sample mean is away from the population mean. It allows us to assess the significance of the difference between the sample mean and the population mean. If the Z-score is large (far from zero), it suggests that the sample mean is significantly different from the population mean, providing evidence for rejecting the null hypothesis in hypothesis testing or indicating wider confidence intervals in estimation.
In summary, the expression plays a crucial role in calculating the Z-score, aiding in the interpretation of sample mean differences and facilitating statistical inference in hypothesis testing and estimation.
Practical Applications
The utility of Z-scores extends across various fields and industries:
- Finance: In finance, Z-scores are used to assess the financial health and risk of companies. For example, Altman’s Z-score is a popular model used to predict bankruptcy by evaluating various financial ratios.
- Education: Z-scores are employed in standardized testing to compare individual scores with the mean and standard deviation of a reference population.
- Healthcare: In healthcare, Z-scores are used in fields such as epidemiology to assess growth and nutritional status by comparing measurements such as height and weight to population norms.
- Quality Control: Z-scores aid in quality control processes by identifying deviations from expected values in manufacturing and production settings.
Conclusion
In conclusion, the Z-score is a versatile and indispensable tool in the realm of statistics. Its ability to standardize data, identify outliers, and facilitate probabilistic calculations makes it invaluable for researchers, analysts, and decision-makers across various domains. By understanding and leveraging the power of Z-scores, one can gain deeper insights into datasets, make informed decisions, and drive meaningful outcomes in both research and practical applications. So, the next time you encounter a dataset, remember the mighty Z-score and its role in unlocking the secrets hidden within the numbers.